堆排序算法

堆排序基本思想

1. 将待排序序列构造成一个大顶堆

2. 排序后，整个序列的最大值就是堆顶的根节点。

3. 将堆顶元素其与末尾元素进行交换，此时末尾元素就为最大值。

4. 然后将剩余 n - 1 个元素重新构造成一个大顶堆，这样会得到 n 个元素的次小值。如此反复执行，便能得到一个有序序列了

   堆排序步骤图解

   要求，给定数组{4,6,8,5,9},使用堆排序方法，升序排列

   ---

   步骤一：构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。

1.假设无序序列原始结构如下:

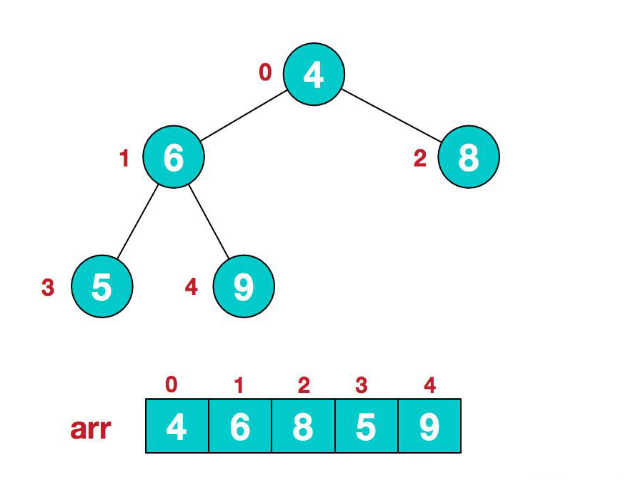
2.此时我们从最后一个非叶子结点开始（叶子结点自然不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1 ，也就是下面的6结点），从左至右，从下至上进行调整。

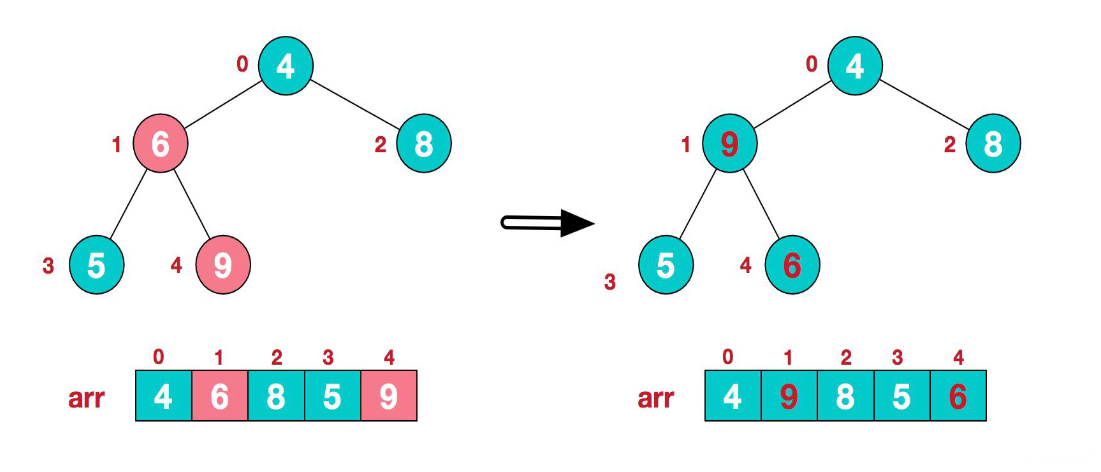
3.找到第二个非叶子节点4，由于[4,9,8]中9元素最大，4和9交换。

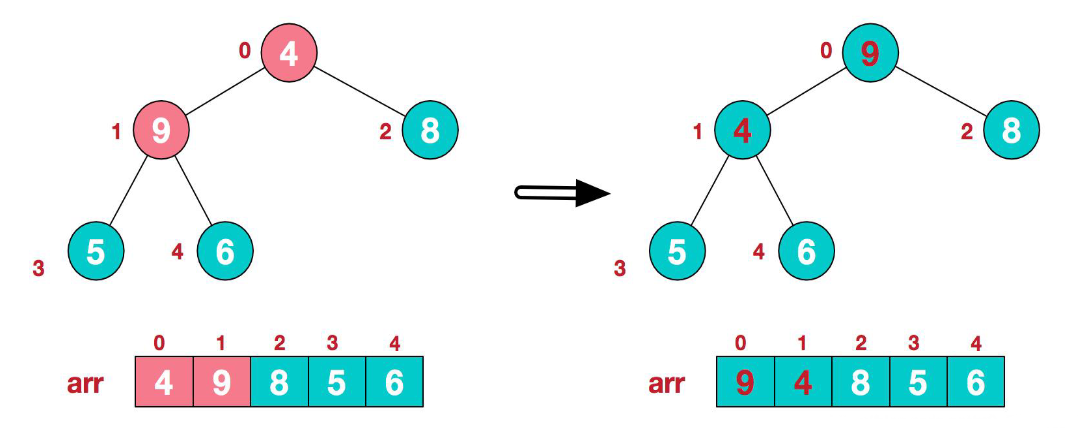
4.此时，第三步交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。

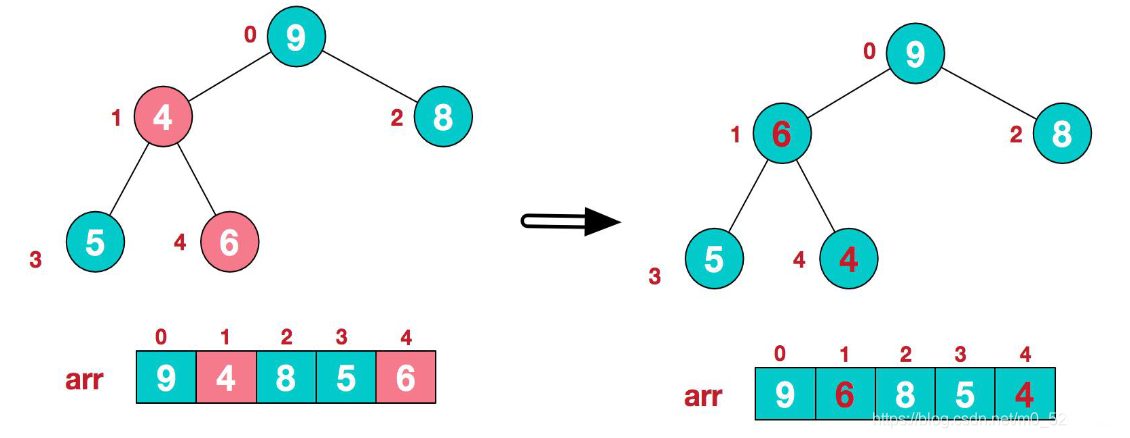
此时，我们就将一个无序序列构造成了一个大顶堆

步骤二：将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

1.将堆顶元素9和末尾元素4进行交换

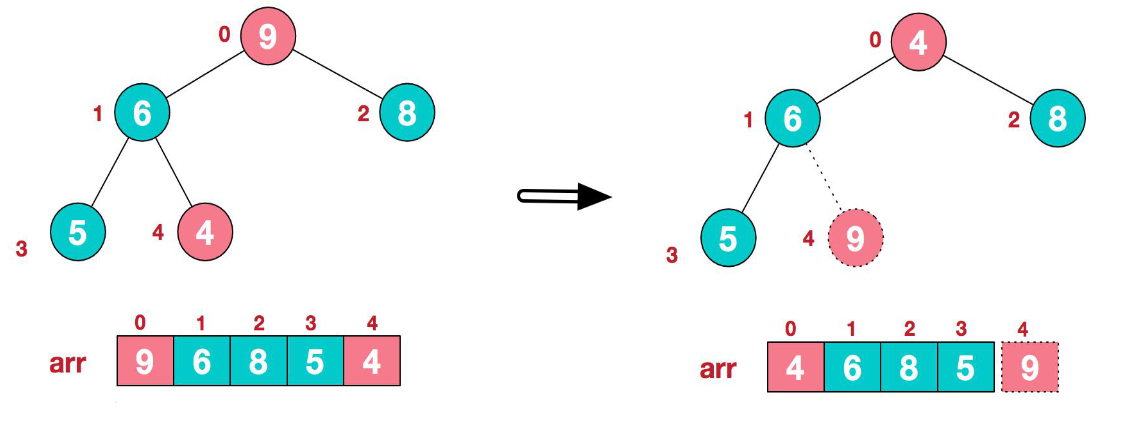
2.重新调整结构，使其继续满足堆定义，此时，堆末尾元素不再参与交换。

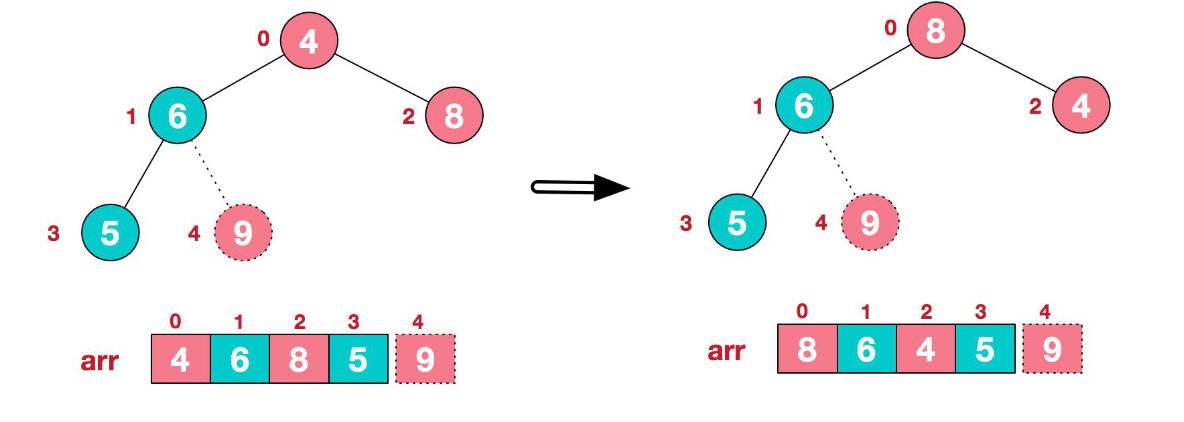
3.再将堆顶元素8与末尾元素5进行交换，得到第二大元素8。

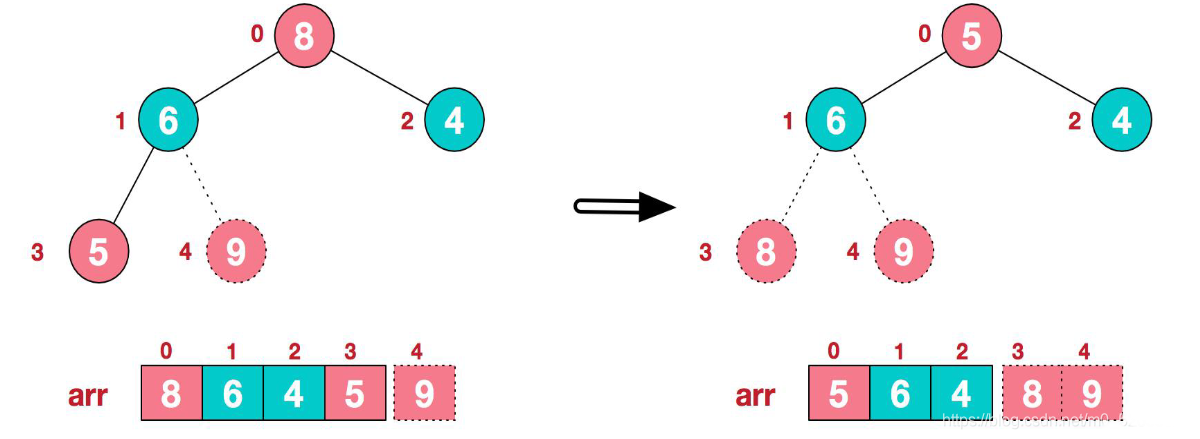
4.后续过程重复上面的操作，继续进行调整，交换，如此反复进行，最终使得整个序列有序。

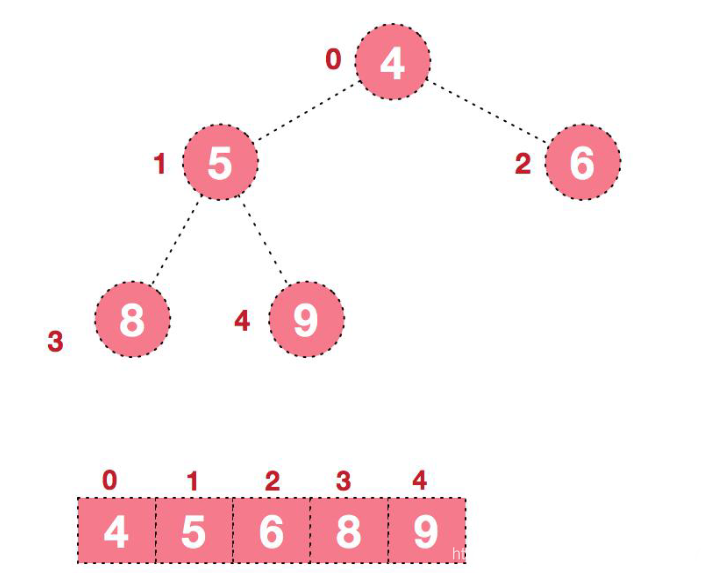
动态图解：

代码实现(Java)

package com.athome.sort;

import java.util.Arrays;
import java.util.Random;

/**
 * Description:
 * Author:江洋大盗
 * Date:2021/1/14 12:30
 */
public class HeapSort {
    /**
     * 此方法将待调整数组调整为符合大顶堆形式的数组
     * @param arr 待调整的数组
     * @param i 表示非叶子节点在数组中的索引
     * @param length 表示对多少个元素进行调整，会不断减小
     */
    public static void adjustHeap(int[] arr,int i,int length){
        //取出非叶子节点对应的值
        int temp = arr[i];
        //开始调整
        for (int j = 2*i+1; j < length; j = 2*j+1) {
            //如果左子节点大于右子节点
            if(j+1 < length && arr[j] < arr[j+1]){
                j++;//指针j指向右子节点
            }
            //如果j指向的值，即i的较大子节点的值大于i指向的父节点的值
            if(arr[j] > temp){
                arr[i] = arr[j];//就将较大子节点的值赋给父节点
                i = j;//!!!!将i指向j指向的值
            }else{
                break;
            }
        }
        //当for循环结束后，我们已经将以i为父结点的树的最大值，放在了最顶端(局部)
        arr[i] = temp;
    }

    /**
     * 编写堆排序的方法
     * @param arr 待排序的数组
     */
    public static void heapSort(int[] arr){
        //1.首先将数组调整为大顶堆的形式
        //注意:终止循环的条件为i >= 0,因为第一个元素即arr[0]肯定是一个非叶子节点，需要调整。
        for (int i = (arr.length-1)/2; i >= 0; i--) {
            adjustHeap(arr,i,arr.length);
        }
        //2.将堆顶元素与末尾元素交换，将最大元素放置在最后
        //注:循环arr.length-1次即可调整好顺序，最后一个元素位置必然正确，不需要调整。
        int temp = 0;//临时变量，做交换用
        for (int i = arr.length-1; i > 0; i--) {
            temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;
            //3.重新调整结构使其满足堆定义，然后继续交换。
            adjustHeap(arr,0,i);
        }
    }
    //测试程序是否正确
    public static void main(String[] args) {
        int[] arr = new int[8];
        Random random = new Random();
        for (int i = 0; i < arr.length; i++) {
            arr[i] = random.nextInt(100);
        }
        System.out.println("排序前:"+ Arrays.toString(arr));
        heapSort(arr);
        System.out.println("排序后:"+ Arrays.toString(arr));

    }
}

测试结果

结语

只要能收获甜蜜，荆棘丛中也有蜜蜂忙碌的身影，未来的你一定会感谢现在努力的自己。