Logo

Menu

一溪风月
一溪风月
Published on 2023-04-27 / 18 Visits
0

树的基础知识(Java)

#数据结构

为什么需要树这种数据结构

数组：

20230427170047.png

优点：通过下标方式访问元素，速度快。对于有序数组，还可使用二分查找提高检索速度 缺点：如果要检索具体某个值，或者插入值(按一定顺序)会整体移动，效率较低[示意图]

链表：

20230427170320.png

优点：在一定程度上对数组存储方式有优化(比如：插入一个数值节点，只需要将插入节点，链接到链表中即可，删除效率也很好) 缺点：在进行检索时，效率仍然较低，比如(检索某个值，需要从头节点开始遍历)。

二叉树

基本说明

  • 每个节点最多只能有两个子节点的一种形式称为二叉树。

  • 二叉树的子节点分为左节点和右节点。

  • 如果该二叉树的所有叶子节点都在最后一层，并且结点总数=2^n^-1,n为层数，则我们称为满二叉树。

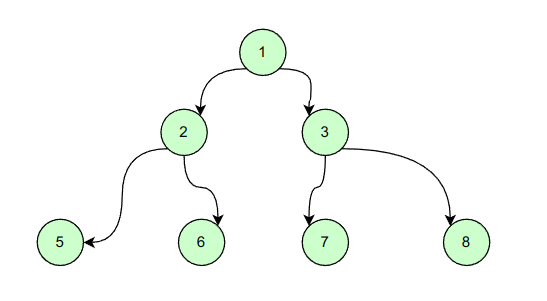
20230427170930.png

  • 如果该二叉树的所有叶子节点都在最后一层或者倒数第二层，而且最后一层的叶子节点在左边连续，倒数第二层的叶子节点在右边连续，我们称为完全二叉树

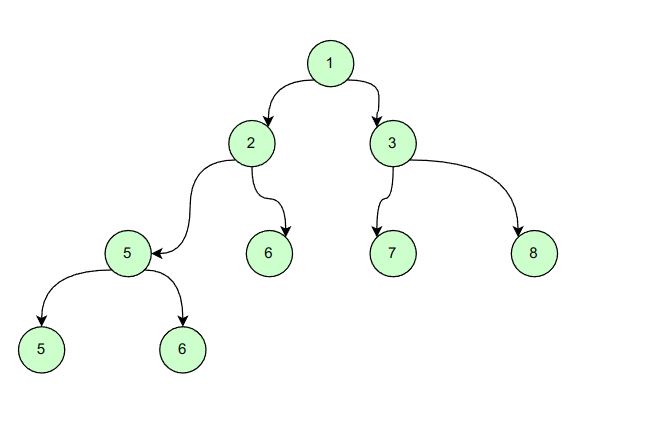
20230427171038.png

二叉树的遍历，查找，线索化等操作。

代码实现:

首先创建一个节点类

package com.athome.binarytree;

/**
 * Description:
 * Author:江洋大盗
 * Date:2021/1/21 11:02
 */
public class HeroNode {
    String name;
    int num;//表示英雄的编号
    HeroNode left;//左子节点
    HeroNode right;//右子节点
    boolean leftType;//表示左节点是否线索化
    boolean rightType;//右节点是否线索化

    public HeroNode(String name, int num) {
        this.name = name;
        this.num = num;
    }

    /**
     * 前序遍历
     */
    public void preorder() {
        System.out.println(this);
        if (this.left != null) {
            this.left.preorder();
        }
        if (this.right != null) {
            this.right.preorder();
        }
    }

    /**
     * 前序查找
     *
     * @param num 待查找的编号
     * @return 返回查找到的节点，若查询不到返回null
     */
    public HeroNode preorderSearch(int num) {
        if (this.num == num) {
            return this;
        }
        HeroNode node = null;
        if (this.left != null) {
            node = this.left.preorderSearch(num);
        }
        if (node != null) {
            return node;
        }
        if (this.right != null) {
            node = this.right.preorderSearch(num);
        }
        return node;
    }

    /**
     * 中序遍历
     */
    public void inorder() {
        if (this.left != null) {
            this.left.inorder();
        }
        System.out.println(this);
        if (this.right != null) {
            this.right.inorder();
        }
    }

    /**
     * 中序查找
     *
     * @param num 待查找的编号
     * @return 返回查找到的节点，若查询不到返回null
     */
    public HeroNode inorderSearch(int num) {
        HeroNode node = null;
        if (this.left != null) {
            node = this.left.inorderSearch(num);
        }
        if (node != null) {
            return node;
        }
        if (this.num == num) {
            return this;
        }
        if (this.right != null) {
            node = this.right.inorderSearch(num);
        }
        return node;
    }

    /**
     * 后序遍历
     */
    public void postorder() {
        if (this.left != null) {
            this.left.postorder();
        }
        if (this.right != null) {
            this.right.postorder();
        }
        System.out.println(this);
    }

    /**
     * 后续查找
     *
     * @param num 待查找的编号
     * @return 返回查找到的节点，若查询不到返回null
     */
    public HeroNode postorderSearch(int num) {
        HeroNode node = null;
        if (this.left != null) {
            node = this.left.postorderSearch(num);
        }
        if (node != null) {
            return node;
        }
        if (this.right != null) {
            node = this.right.postorderSearch(num);
        }
        if (this.num == num) {
            return this;
        }
        return node;
    }

    @Override
    public String toString() {
        return "HeroNode{" +
                "姓名: '" + name + ''' +
                ", 排名: " + num +
                '}';
    }
}

创建二叉树的类，实现遍历和查找：

package com.athome.binarytree;

/**
 * Description:
 * Author:江洋大盗
 * Date:2021/1/21 11:13
 */
public class BinaryTree {
    HeroNode root;

    /**
     * 前序遍历
     */
    public void preorder() {
        if (root == null) {
            return;
        }
        root.preorder();
    }

    /**
     * 前序查找
     *
     * @param num 待查找的编号
     * @return 返回查找到的节点，若查询不到返回null
     */
    public HeroNode preorderSearch(int num) {
        if (root == null) {
            return null;
        }
        return root.preorderSearch(num);
    }

    /**
     * 中序遍历
     */
    public void inorder() {
        if (root == null) {
            return;
        }
        root.inorder();
    }

    /**
     * 中序查找
     *
     * @param num 待查找的编号
     * @return 返回查找到的节点，若查询不到返回null
     */
    public HeroNode inorderSearch(int num) {
        if (root == null) {
            return null;
        }
        return root.inorderSearch(num);
    }

    /**
     * 后序遍历
     */
    public void postorder() {
        if (root == null) {
            return;
        }
        root.postorder();
    }

    /**
     * 后续查找
     *
     * @param num 待查找的编号
     * @return 返回查找到的节点，若查询不到返回null
     */
    public HeroNode postorderSearch(int num) {
        if (root == null) {
            return null;
        }
        return root.postorderSearch(num);
    }
}

顺序存储二叉树： 基本介绍： 从数据存储来看，数组存储方式和树的存储方式可以相互转换，即数组可以转换成树，树也可以转换成数组。

顺序存储二叉树的特点:

  • 顺序二叉树通常只考虑完全二叉树

  • 第n个元素的左子节点为2^n^+1

  • 第n个元素的右子节点为2^n^+2

  • 第n个元素的父节点为(n-1)/2

  • n:表示二叉树中的第几个元素(按0开始编号如图所示)

package com.athome.binarytree;

/**
 * Description:
 * Author:江洋大盗
 * Date:2021/1/21 14:30
 */
public class SequentialStorage {
    private final int[] arr;

    public SequentialStorage(int[] arr) {
        this.arr = new int[arr.length];
        System.arraycopy(arr, 0, this.arr, 0, arr.length);
    }

    /**
     * 重载前序遍历
     */
    public void preorder() {
        preorder(0);
    }

    /**
     * @param index 开始遍历的角标
     */
    private void preorder(int index) {
        if (arr.length == 0) {
            System.out.println("数组为空");
            return;
        }
        System.out.println(arr[index]);
        if (2 * index + 1 < arr.length) {
            preorder(2 * index + 1);
        }
        if (2 * index + 2 < arr.length) {
            preorder(2 * index + 2);
        }
    }

    /**
     * 重载中序遍历
     */
    public void inorder() {
        inorder(0);
    }

    /**
     * @param index 开始遍历的角标
     */
    private void inorder(int index) {
        if (arr.length == 0) {
            System.out.println("数组为空");
            return;
        }
        if (2 * index + 1 < arr.length) {
            inorder(2 * index + 1);
        }
        System.out.println(arr[index]);
        if (2 * index + 2 < arr.length) {
            inorder(2 * index + 2);
        }
    }

    /**
     * 重载后序遍历
     */
    public void postorder() {
        postorder(0);
    }

    /**
     * @param index 开始遍历的角标
     */
    private void postorder(int index) {
        if (arr.length == 0) {
            System.out.println("数组为空");
            return;
        }
        if (2 * index + 1 < arr.length) {
            postorder(2 * index + 1);
        }
        if (2 * index + 2 < arr.length) {
            postorder(2 * index + 2);
        }
        System.out.println(arr[index]);
    }
}

创建线索化二叉树的类

package com.athome.binarytree;

/**
 * Description:
 * Author:江洋大盗
 * Date:2021/1/21 14:45
 */
public class ThreadBinaryTree {
    private HeroNode root;//根节点
    private HeroNode pre;

    public ThreadBinaryTree(HeroNode root) {
        this.root = root;
    }

    /**
     * 中序线索化
     *
     * @param node 开始线索化的节点
     */
    private void inThread(HeroNode node) {
        if (node == null) {
            return;
        }
        //1.线索化左子树
        inThread(node.left);
        //2.线索化当前节点
        if (node.left == null) {
            node.left = pre;
            node.leftType = true;
        }
        if (pre != null && pre.right == null) {
            pre.right = node;
            pre.rightType = true;
        }
        pre = node;
        //3.线索化右子树
        inThread(node.right);
    }

    /**
     * 重载中序线索化方法
     */
    public void inThread() {
        pre = null;
        inThread(root);
    }

    /**
     * 中序遍历线索化二叉树
     */
    public void inorder() {
        HeroNode node = root;
        while (node != null) {
            while (!node.leftType) {
                node = node.left;
            }
            System.out.println(node);
            while (node.rightType) {
                node = node.right;
                System.out.println(node);
            }
            node = node.right;
        }
    }

    /**
     * 前序线索化二叉树
     *
     * @param node 开始线索化的节点
     */
    private void preThread(HeroNode node) {
        if (node == null) {
            return;
        }
        //1.线索化当前节点
        if (node.left == null) {
            node.left = pre;
            node.leftType = true;
        }
        if (pre != null && pre.right == null) {
            pre.right = node;
            pre.rightType = true;
        }
        pre = node;
        //2.线索化左子树
        if (!node.leftType) {
            preThread(node.left);
        }
        //线索化右子树
        if (!node.rightType) {
            preThread(node.right);
        }
    }

    /**
     * 重载前序线索化的方法
     */
    public void preThread() {
        pre = null;
        preThread(root);
    }

    /**
     * 前序遍历线索化二叉树
     */
    public void preorder() {
        HeroNode node = root;
        while (node != null) {
            while (!node.leftType) {
                System.out.println(node);
                node = node.left;
            }
            System.out.println(node);
            node = node.right;
        }
    }

    /**
     * 后续线索化二叉树
     *
     * @param node 开始线索化的节点
     */
    private void postThread(HeroNode node) {
        if (node == null) {
            return;
        }
        //1.线索化左子树
        postThread(node.left);
        //2.线索化右子树
        postThread(node.right);
        //3.线索化当前节点
        if (node.left == null) {
            node.left = pre;
            node.leftType = true;
        }
        if (pre != null && pre.right == null) {
            pre.right = node;
            pre.rightType = true;
        }
        pre = node;
    }

    /**
     * 重载后续线索化方法
     */
    public void postThread() {
        pre = null;
        postThread(root);
    }

    /**
     * 后续遍历线索二叉树，（暂时想不出好的解法）
     */
    public void postorder() {

    }
}

结语

只要能收获甜蜜，荆棘丛中也有蜜蜂忙碌的身影，未来的你一定会感谢现在努力的自己。

马踏棋盘算法（使用贪心算法优化）（...
常见排序算法的实现与总结(Java)